The equation of parabola in vertex form is
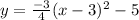
Solution:
Given that parabola with vertex (3, -5) and going through point (1, -8)
To find : equation of parabola
The equation of parabola in vertex form is given as:
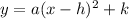 ----- eqn 1
----- eqn 1
where (h, k) are the coordinates of the vertex
here (h, k) = (3, −5)
Substituting the values in above formula, we get
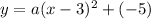
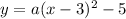 ----- eqn 2
----- eqn 2
The given equation of parabola passes through (1, -8)
Substituiting (x, y) = (1, -8) in eqn 2 we get,
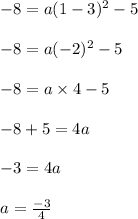
Now substitute the value of "a" in eqn 2,
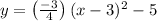
Thus the equation of parabola in vertex form is found