Question

What are the discontinuity and zero of the function f(x) = quantity x squared plus 6 x plus 8 end quantity over quantity x plus 4

Discontinuity at (4, 6), zero at (−2, 0)

Discontinuity at (4, 6), zero at (2, 0)

Discontinuity at (−4, −2), zero at (−2, 0)

Discontinuity at (−4, −2), zero at (2, 0)

Answer 1

Discontinuity at (-4,-2), zero at (-2,0).

Explanation:

We are given that a function

`f(x)=(x^2+6x+8)/(x+4)`

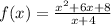
We have to find the discontinuity and zero of the given function.

Discontinuity: It is that point where the function is not defined.

It makes the function infinite.

`f(x)=(x^2+4x+2x+8)/(x+4)`

`f(x)=((x+4)(x+2))/(x+4)`

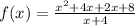
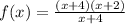
When x=-4 then

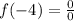`f(-4)=(0)/(0)` It is indeterminate form

Function is not defined

After cancel out x+4 in numerator and denominator then we get

`f(x)=x+2`

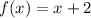
Substitute x=-4

`f(-4)=-4+2=-2`

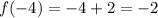
Therefore, the point of discontinuity is (-4,-2).

Zero: The zero of the function is that number when substitute it in the given function then the function becomes zero.

When substitute x=-2

Then ,
`f(0)=-2+2=0`

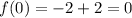
The function is zero at (-2,0).

Hence, option C is true.