Answer:
Discontinuity at (-4,-2), zero at (-2,0).
Explanation:
We are given that a function
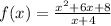
We have to find the discontinuity and zero of the given function.
Discontinuity: It is that point where the function is not defined.
It makes the function infinite.
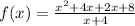
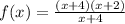
When x=-4 then
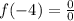 It is indeterminate form
It is indeterminate form
Function is not defined
After cancel out x+4 in numerator and denominator then we get

Substitute x=-4
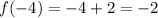
Therefore, the point of discontinuity is (-4,-2).
Zero: The zero of the function is that number when substitute it in the given function then the function becomes zero.
When substitute x=-2
Then ,
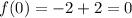
The function is zero at (-2,0).
Hence, option C is true.