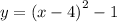The vertex is (4, -1) and contains the point (2, 3)

Question

asked Apr 16, 2022 104k views

1 Answer

Richard Kuo · Answer 1 · 2022-04-22T12:43:05+0000

Answer:

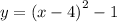
$y = {(x - 4)}^(2) - 1$

Explanation:

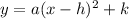
y = a(x - h)^(2) + k

We know the value of h and k.

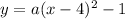
y = a(x - 4)^(2) - 1

The graph passes through (2,3). Therefore, substitute x = 2 and y = 3.

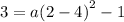
$3 = a {(2 - 4)}^(2) - 1$

Solve for a.

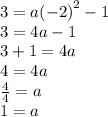
$3 = a {( - 2)}^(2) - 1 \\ 3 = 4a - 1 \\ 3 + 1 = 4a \\ 4 = 4a \\ (4)/(4) = a \\ 1 = a$

Therefore, a = 1. Rewrite the equation.

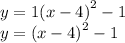
$y = 1 {( x - 4)}^(2) - 1 \\ y = {(x - 4)}^(2) -1$

Answer Check

Substitute x = 2 and y = 3 in the equation.

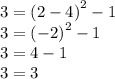
$3 = {(2 - 4)}^(2) - 1 \\ 3 = {( - 2)}^(2) - 1 \\ 3 = 4 - 1 \\ 3 = 3$

The equation is true for (2,3). Therefore, the answer is —

$y = {(x - 4)}^(2) - 1$