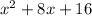Question

What constant term is necessary to complete the

perfect square trinomial pictured in the algebra tiles?
x2 + 8x +​

Answer 1

Answer: x^2 + 8x + 16

Explanation:

I did it on Edge and got it right!

Answer 2

The complete expression is
`x^2 + 8x + 16`

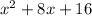
So the missing term is 16.

Explanation:

Here, the given expression is:
`x^2 + 8x +`

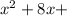
Let us assume the missing term =
`k^2`

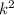
So, the given expression becomes
`x^2 + 8x + k^2`

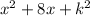
Now, by ALGEBRAIC IDENTITY:

`(a +b)^2 = a^2 + b^2 + 2ab`

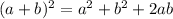
So, here applying this identity, we get

`a^2  + 2ab + b^2   = x^2 + 8x + k^2`

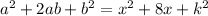
So on comparing, we get

`a^2 = x^2, b^2  = k^2,  2 ab = 8x = 2 (x) (4)`

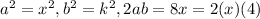
So, we get that 2 (x) (4) = 2 (a)(b)

⇒ a = x, b= 4

`\implies (a+b)^2  = (x+4)^2`

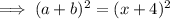
So, the missing term is
`k^2 = b^2 = (4)^2 = 16`

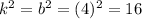
Hence, the complete expression is
`x^2 + 8x + 16`