Question

Which table represents a linear function?

Answer 1

As the tables are not attached, the attachment is given below:

Answer:

Only table 3 represents the linear function.

Explanation:

The linear equation with slope 'm' and intercept 'c' is given as:

`y = mx + c`

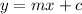
The slope of a line with points
`\left( {{x_1},{y_1}} \right) and \left( {{x_2},{y_2}} \right)` is given as:

`m = (y_2 - y_1)/(x_2 - x_1)`

Table 1:

The slope is calculated as below:

`\begin{aligned}m&=\frac{{ - 6 + 2}}{{2 - 1}}\\&=\frac{{ - 4}}{1}\\&= - 4\\\end{aligned}`

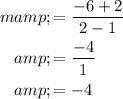
The slope of other two points can be obtained as follows,

`\begin{aligned}m&= \frac{{ - 2 + 6}}{{3 - 2}}\\&= (4)/(1)\\&=4\\\end{aligned}`

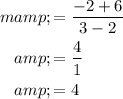
The slopes are not equal. Therefore, table 1 is not correct.

Table 2:

The slope is calculated as below:

`\begin{aligned}m&= \frac{{ - 5 + 2}}{{2 - 1}}\\&=\frac{{ - 3}}{1}\\&= - 3\\\end{aligned}`

The slope of other two points can be obtained as follows,

`\begin{aligned}m&=\frac{{ - 9 + 5}}{{3 - 2}}\\&= \frac{{ - 4}}{1}\\&= - 4\\\end{aligned}`

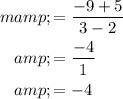
The slopes are not equal. Therefore, table 2 is not correct.

Table 3:

The slope is calculated as below:

`\begin{aligned}m&= \frac{{ - 10 + 2}}{{2 - 1}}\\&= \frac{{ - 8}}{1}\\&= - 8\\\end{aligned}`

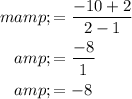
The slope of other two points can be obtained as follows,

`\begin{aligned}m&= \frac{{ - 18 + 10}}{{3 - 2}}\\&= \frac{{ - 8}}{1}\\&= - 8\\\end{aligned}`

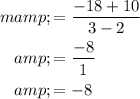
The slopes are equal. Therefore, table 3 is correct.

Table 4:

The slope is calculated as below:

`\begin{aligned}m&= \frac{{ - 4 + 2}}{{2 - 1}}\\&=\frac{{ - 2}}{1}\\&= - 2\\\end{aligned}`

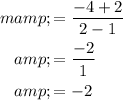
The slope of other two points can be obtained as follows,

`\begin{aligned}m&=\frac{{ - 8 + 4}}{{3 - 2}}\\&= \frac{{ - 4}}{1}\\&= - 4\\\end{aligned}`

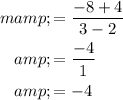
The slopes are not equal. Therefore, table 4 is not correct.

Therefore, only table 3 represents the linear function.