Question

How many ounces of a 32%

alcohol solution and a 38%
alcohol solution must be combined to obtain 87
ounces of a 34% solution?

Answer 1

58 ounces of 32% solution and 29 ounces of 38% solution should be mixed.

Explanation:

Let, 87 ounces of a 34% solution is prepared by mixing x ounces of 32% alcohol solution and y ounces of 38% alcohol solution.

Hence, x + y = 87 .......... (1)

And,
`((32x)/(100) + (38y)/(100))/(x + y) = (34)/(100)`

⇒
`(32x)/(100) + (38y)/(100) = (34 * 87)/(100)`

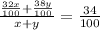
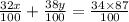
⇒ 0.32x + 0.38y = 29.58

⇒ x + 1.1875 y = 92.4375 ......... (2)

Now, from equations (1) and (2) we get

(1.1875 - 1)y = 92.4375 - 87

⇒ y = 29

Hence, from equation (1) we get, x = 87 - 29 = 58

Therefore, 58 ounces of 32% solution and 29 ounces of 38% solution should be mixed. (Answer)