Points:
The question is incomplete as the value of x is not given and what is required is not stated.
However, I'll assume that x = 5
Going by the details of the question, possible questions could be:
- Expected number of hits
- Variance and Standard Deviation of hits
Answer:
See Explanation
Explanation:
Given
Represent the probability with p.
So:
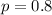
Solving (a): The expected number of hits.
In probability, the expected number is calculated as:
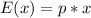
Substitute values for p and x
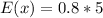
Remember that 5 is an assumed value of x
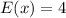
Hence, the expected number of hits when 5 missiles is fired is 4
Solving (b): Variance
In probability, variance is calculated as:
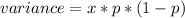
Substitute values for p and x
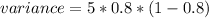


Hence, the variance is 0.8
Solving (c): The standard deviation
In probability, the standard deviation is calculated as:
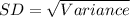
Substitute values for variance
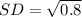
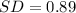
Hence, the standard deviation is 0.89