Answer:
The sample should be 1,068.
Explanation:
Consider the provided information.
Confidence level is 95% and margin of error is 0.03.
Thus,
1-α=0.95
α=0.05, E=0.03 and planning value
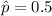
Formula to calculate sample size is:

From the table we can find:
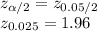
Substitute the respective values in the above formula we get:
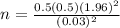
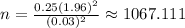
Hence, the sample should be 1,068.