Question

At 95% confidence, how large a sample should be taken to obtain a margin of error of .03 for the estimation of the population proportion? Assume past data are not available for developing a planning value for p*.

Answer 1

The Answer should really be 1,068.

Answer 2

The sample should be 1,068.

Explanation:

Consider the provided information.

Confidence level is 95% and margin of error is 0.03.

Thus,

1-α=0.95

α=0.05, E=0.03 and planning value
`\hat p=0.5`

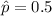
Formula to calculate sample size is:
`n=(\hat p(1-\hat p)(z_(\alpha/2))^2)/(E^2)`

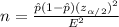
From the table we can find:

`z_(\alpha/2)=z_(0.05/2)\\z_(0.025)=1.96`

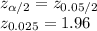
Substitute the respective values in the above formula we get:

`n=(0.5(0.5)(1.96)^2)/((0.03)^2)`

`n=(0.25(1.96)^2)/((0.03)^2)\approx 1067.111`

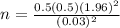
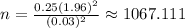
Hence, the sample should be 1,068.