Answer:
623,459.79 and 224.51
Step-by-step explanation:
first lets consider the first part of the problem and is how mucho do i need to accumulate for having an annuity for 25 years. this problem can be solved applying the concept of annuity, keep in mind that an annuity is a formula which allows you to calculate the present value of future payments affected by an interest rate.by definition the present value of an annuity is given by:
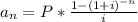
where
 is the present value of the annuity,
is the present value of the annuity,
 is the interest rate for every period payment, n is the number of payments, and P is the regular amount paid. so applying to this particular problem, we have:
is the interest rate for every period payment, n is the number of payments, and P is the regular amount paid. so applying to this particular problem, we have:
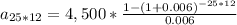
look at the value 25*12 because the problem tells us is during 25 years but the payment is monthly, and look at the 0.006 and it is comming from the APR/12 and we must do that because this rate is componded Monthly:

so for the second part we must calculate the second part we must calculate the acumulated value at 40 years of work:
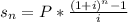
where
 is the future value of the annuity,
is the future value of the annuity,
 is the interest rate for every period payment, n is the number of payments, and P is the regular amount paid. so applying to this particular problem, we have:
is the interest rate for every period payment, n is the number of payments, and P is the regular amount paid. so applying to this particular problem, we have:
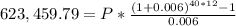
solving for P we have:
P=224.51