Answer:
T= 6.78 10⁷ s
Step-by-step explanation:
One way to accomplish this problem is to use Kepler's third law, which relates the order of the planets to their orbital distance.
T² = (4π² / G
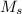 ) a³
) a³
Where T and a are the period and orbital radius, respectively
Let's start by writing the data for Earth and the new planet
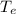 ² = (4π² / G
² = (4π² / G
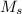 ) ae³
) ae³
T² = (4pi2 / G
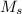 ) a³
) a³
Let's solve with these equations
T² /
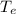 ²2 = a³ /
²2 = a³ /
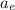 ³
³
T² =
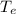 ² (a /
² (a /
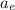 )³
)³
The land period is 1 year
Te = 1 year (365 days / 1 year) (24h / 1 day) (3600s / 1h)
Te = 3.15 10⁷ s
Let's calculate
T² = (3.15 107)² (2.5 1011 / 1.5 1011) 3
T = RA 45.94 10¹⁴ s
T= 6.78 10⁷ s