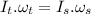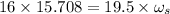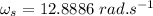Question

A gymnast is in a tucked position to complete her somersaults. While tucked her moment of inertia about an axis through the center of her body is 16.0 kg-m² and she rotates at 2.5 rev/s. When she kicks out of her tuck into a straight position, her moment of inertia becomes 19.5 kg-m². What is her rate of rotation after she straightens out?

Answer 1

`\omega_s=12.8886\ rad.s^(-1)`

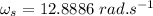
Step-by-step explanation:

Given that:

• moment of inertia of tucked body,
  `I_t=16\ kg.m^2`

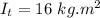
• rotational speed of the body,
  `N_t=2.5\ rev.s^(-1)`

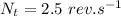
• i.e.
  `\omega_t=2\pi* 2.5=15.708\ rad.s^(-1)`

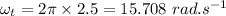
• moment of inertia of the straightened body,
  `I_s=19.5\ kg.m^2`

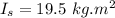
Now using the law of conservation of angular momentum:

angular momentum of tucked body=angular momentum of straight body

`I_t.\omega_t=I_s.\omega_s`

`16* 15.708=19.5* \omega_s`

`\omega_s=12.8886\ rad.s^(-1)`