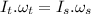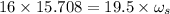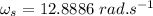Answer:
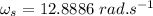
Step-by-step explanation:
Given that:
- moment of inertia of tucked body,
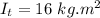
- rotational speed of the body,
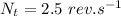
- i.e.
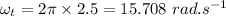
- moment of inertia of the straightened body,
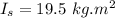
Now using the law of conservation of angular momentum:
angular momentum of tucked body=angular momentum of straight body