Question

The escape velocity on earth is 11.2 km/s. What fraction of the escape velocity is the rms speed of H2 at a temperature of 31.0 degrees Celsius on the earth? Note that virtually all the molecules will have escaped the earth's atmosphere if this fraction exceeds 0.15.

Answer 1

To solve this problem it is necessary to apply the concept related to root mean square velocity, which can be expressed as

`v_(rms) = \sqrt{(3RT)/(n)}`

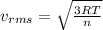
Where,

T = Temperature

R = Gas ideal constant

n = Number of moles in grams.

Our values are given as

`v_e =11.2km/s = 11200m/s`

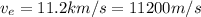
The temperature is

`T = 30\°C = 30+273 = 303K`

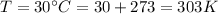
Therefore the root mean square velocity would be

`v_(rms) = \sqrt{(3(8.314)(303))/(0.002)}`

`v_(rms) = 1943.9m/s`

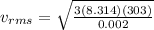
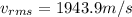
The fraction of velocity then can be calculated between the escape velocity and the root mean square velocity

`\alpha = (v_(rms))/(v_e)`

`\alpha = (1943.9)/(11200)`

`\alpha = 0.1736`

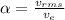
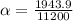
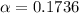
Therefore the fraction of the scape velocity on the earth for molecula hydrogen is 0.1736