Question

The base of an isosceles triangle is one and a half times the length of the other two sides.A smaller triangle has a perimeter that is half the perimeter of the first. Write an expression for the perimeter of the smaller triangle and combine like terms. What is the simplified expression?

Answer 1

Perimeter of the smaller triangle = 1.75x

Explanation:

Let the two equal sides of an isosceles triangle = x

Therefore, length of the base =
`(1(1)/(2))x`

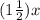
Perimeter of this isosceles triangle = x + x +
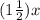
`(1(1)/(2))x`

= 2x +
`(1+(1)/(2))x`

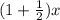
= 2x + x +
`(x)/(2)`

=
`(5x)/(2)`

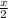
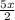
Since, smaller triangle has a perimeter that is half the perimeter of the larger triangle,

Length of each corresponding side of smaller triangle will be half of the larger triangle.

Length of sides of the smaller triangle =
`(x)/(2),(x)/(2),(1(1)/(2))(x)/(2)`

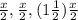
Perimeter of the smaller triangle =
`(x)/(2)+(x)/(2)+(1(1)/(2))(x)/(2)`

= x +
`(x)/(2)+(x)/(4)`

=
`(3)/(2)x+(x)/(4)`

=
`(6)/(4)x+(x)/(4)`

=
`(7)/(4)x`

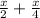
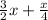
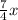
= 1.75x

Therefore, expression that represents the perimeter of the smaller triangle is (1.75x)