Question

Find the area and perimeter of ABC at right. Give approximate (decimal) answers, not exact answers

Answer 1

Area of Δ ABC = 21.86 units square

Perimeter of Δ ABC = 24.59 units

Explanation:

Given:

In Δ ABC

∠A=45°

∠C=30°

Height of triangle = 4 units.

To find area and perimeter of triangle we need to find the sides of the triangle.

Naming the end point of altitude as 'O'

Given
`BO\perp AC`

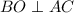
For Δ ABO

Since its a right triangle with one angle 45°, it means it is a special 45-45-90 triangle.

The sides of 45-45-90 triangle is given as:

We are given BO (Leg 1)
`x=4`

∴ AO (Leg2)
`=x=4`

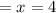
∴ AB (hypotenuse)
`=x\sqrt2=4\sqrt2=5.66`

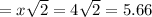
For Δ CBO

Since its a right triangle with one angle 30°, it means it is a special 30-60-90 triangle.

The sides of 30-60-90 triangle is given as:

We are given BO (side opposite 30° angle)
`=x=4`

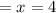
CO (side opposite 60° angle)
`=x\sqrt3=4\sqrt3=6.93`

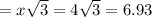
BC (Hypotenuse)
`=2x=2* 4 =8`

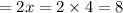
Length of side AC is given as sum of AO and CO

`AC=AO+CO=4+6.93=10.93`

Perimeter of Δ ABC= Sum of sides of triangle

⇒ AB+BC+AC

⇒
`5.66+8+10.93`

⇒
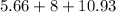
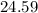`24.59` units

Area of Δ ABC =
`(1)/(2)* base* height`

⇒
`(1)/(2)* 10.93* 4`

⇒
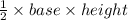
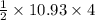
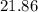`21.86` units square