Question

A ray of light is incident on a flat surface of a block of polystyrene, with an index of refraction of 1.49, that is submerged in water. The ray is split at the surface, where the angle of refraction of the transmitted ray is 18.6°. What is the angle of reflection (in degrees) of the reflected ray?

Answer 1

To solve this problem it is necessary to apply the Snell Law. With which the angles of refraction and incidence on two materials with a determined index of refraction are described.

The equation stipulates that

`n_1 sin\theta_1 = n_2 sin\theta_2`

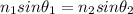
Where,

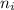`n_i`= Index of refraction of each material

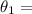`\theta_1 =` Angle of incidence or Angle of Reflection

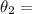`\theta_2 =` Angle of refraction

Our values are given as,

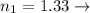`n_1 = 1.33 \rightarrow` Index of refraction of water

`n_2 = 1.49`

`\theta = 18.6\°`

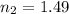
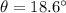
Replacing we have that,

`n_1 sin\theta_1 = n_2 sin\theta_2`

`(1.33) sin\theta_1 = (1.49)sin18.6`

`\theta_1 = sin^(-1) (((1.49)sin18.6)/(1.33))`

`\theta_1 = 20.93\°`

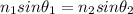
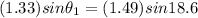
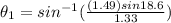
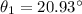
Therefore the angle of reflection is 20.93°