Answer:
R = 0.001 m
Step-by-step explanation:
Continuity equation
The continuity equation is nothing more than a particular case of the principle of conservation of mass. It is based on the flow rate (Q) of the fluid must remain constant throughout the entire pipeline.
Flow Equation
Q = v*A
where:
Q = Flow in (m³/s)
A is the surface of the cross sections of points 1 and 2 of the duct.
v is the flow velocity at points 1 and 2 of the pipe.
It can be concluded that since the Q must be kept constant throughout the entire duct, when the section (A) decreases, the speed (v) increases in the same proportion and vice versa.
Data
D₂= 0.001 m² : final hose diameter
v₁ = 5 m/s : initial speed of fluid
v₂ = 20 m/s : final speed of fluid
Area calculation
A = (π*D²)/4
A₁ = (π*D₁²)/4
A₂ = (π*D₂²)/4
Continuity equation
Q₁ = Q₂
v₁A₁ = v₂A₂
v₁(π*D₁²)/4 = v₂(π*D₂²)/4 : We divide by (π/4) both sides of the equation
v₁ (D₁)² = v₂(D₂)²
We replace data
5 *(D₁)² = 20*(0.001)²
(D₁)² = (20/5)*(0.001)²
(D₁)² = 4*10⁻⁶ m²
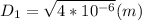
D₁ = 2*10⁻³ m : diameter of the hose
Radius of the hose(R)
R= D₁/2
R= (2*10⁻³ m) / 2
R= (1*10⁻³ m) = 0.001 m