Answer:
Binomial; \mu p=87.5, \sigma p=7.542
Explanation:
- a distribution is said be a binomial distribution iff
- The probability of success of that event( let it be p) is same for every trial
- each trial should have 2 outcome : p or (1-p) i.e, success or failure only.
- there are fixed number of trials (n)
- the trials are independent
- here, the trials are obviously independent ( because, one person's debt doesn't influence the other person's)
- the probability of success(0.35) is same for every trial
(35/100=0.35 is the required p here)
[since, the formula for
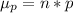 ]
]
[since, the formula for [tex]\sigma _{p} =\sqrt{n*(p)*(1-p)}
- therefore, it is Binomial; \mu p=87.5, \sigma p=7.542