Question

20 Points NEED HELP ASAP

Which statements describe the end behavior of the graph of the function shown? Check all that apply.

f(x)=(x-2)(x+1) /x+1


A As x → ∞, y → 1.

B As x → ∞, y → ∞.

C As x → ∞, y → –∞.

D As x → –∞, y → 1.

E As x → –∞, y → ∞.

F As x → –∞, y → –∞


CHECK ALL THAT APPLY

Answer 1

A B C

X can't be equal to - 1

Answer 2

There are 2 answers: choice B and choice F

==========================================

Step-by-step explanation:

Assuming the second "x+1" is all in the denominator, this will cancel with the first "x+1" in the numerator. I'm using the rule that x/x = 1 where x is nonzero.

What happens after the canceling is that f(x) = x-2. This is a linear equation with positive slope (the slope is 1).

The positive slope means the line goes up as we read it from left to right. As x gets larger, y does too. So we can say
`\text{ as } x \to \infty \text{ , } y \to \infty`

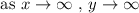
Going in reverse, as x heads off to negative infinity, y does the same as well. Therefore,
`\text{as } x \to -\infty \text{ , } y \to -\infty`

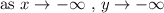
Below is the graph attached as an image to help visually verify the two answers. Note the hole at x = -1 which is due to the fact that this x value makes the original unsimplified version of f(x) to be undefined. Recall that we cannot divide by zero so x+1 cannot be equal to zero.