There are 2 answers: choice B and choice F
==========================================
Step-by-step explanation:
Assuming the second "x+1" is all in the denominator, this will cancel with the first "x+1" in the numerator. I'm using the rule that x/x = 1 where x is nonzero.
What happens after the canceling is that f(x) = x-2. This is a linear equation with positive slope (the slope is 1).
The positive slope means the line goes up as we read it from left to right. As x gets larger, y does too. So we can say
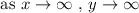
Going in reverse, as x heads off to negative infinity, y does the same as well. Therefore,
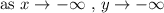
Below is the graph attached as an image to help visually verify the two answers. Note the hole at x = -1 which is due to the fact that this x value makes the original unsimplified version of f(x) to be undefined. Recall that we cannot divide by zero so x+1 cannot be equal to zero.