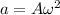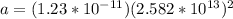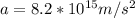Question

Atoms in a solid are not stationary, but vibrate about their equilibrium positions. Typically, the frequency of vibration is about f = 4.11 x 1012 Hz, and the amplitude is about 1.23 x 10^-11 m. For a typical atom, what is its (a) maximum speed and (b) maximum acceleration

Answer 1

To develop this problem it is necessary to use the equations of description of the simple harmonic movement in which the acceleration and angular velocity are expressed as a function of the Amplitude.

Our values are given as

`f = 4.11 *10^(12) Hz`

`A = 1.23 * 10^(-11)m`

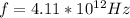
The angular velocity of a body can be described as a function of frequency as

`\omega = 2\pi f`

`\omega = 2\pi 4.11 *10^(12)`

`\omega=2.582*10^(13) rad/s`

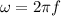
PART A) The expression for the maximum angular velocity is given by the amplitude so that

`V = A\omega`

`V =( 1.23 * 10^(-11))(2.582*10^(13))`

`V =  = 317.586m/s`

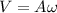
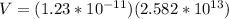
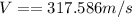
PART B) The maximum acceleration on your part would be given by the expression

`a = A \omega^2`

`a =( 1.23 * 10^(-11))(2.582*10^(13))^2`

`a= 8.2*10^(15)m/s^2`