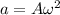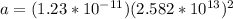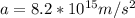To develop this problem it is necessary to use the equations of description of the simple harmonic movement in which the acceleration and angular velocity are expressed as a function of the Amplitude.
Our values are given as
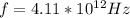
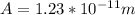
The angular velocity of a body can be described as a function of frequency as
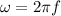
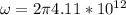

PART A) The expression for the maximum angular velocity is given by the amplitude so that
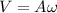
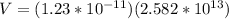
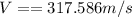
PART B) The maximum acceleration on your part would be given by the expression