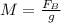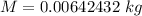Answer:

Step-by-step explanation:
Given:
- mass of deflated balloon,
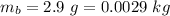
- density of helium,
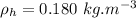
- volume of inflation,
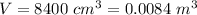
- density of air,
To stop this balloon from rising up we need to counter the buoyant force.
mass of balloon after inflation:
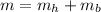
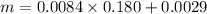
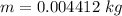
Now the density of inflated balloon:


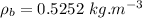
Now the buoyant force on balloon
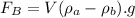
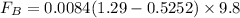
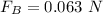
∴Mass to be hung: