Question

A random variable x has a Normal distribution with an unknown mean and a standard deviation of 12. Suppose that we take a random sample of size n = 36 and find a sample mean of ¯ x = 98 . What is a 95% confidence interval for the mean of x ?

Answer 1

Answer: The 95% confidence interval for the mean of x is (94.08, 101.92) .

Explanation:

We are given that ,

A random variable x has a Normal distribution with an unknown mean and a standard deviation of 12.

i.e.
`\sigma= 12`

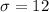
Also, it is given that , Sample mean
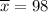`\overline{x}=98` having sample size : n= 36

For 95% confidence ,

Significance level :
`\alpha=1-0.95=0.05`

By using the z-value table , the two-tailed critical value for 95% Confidence interval :

`z_(\alpha/2)=z_(0.025)=1.96`

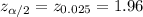
We know that the confidence interval for unknown population mean
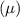`(\mu)` is given by :-

`\overline{x}\pm z_(\alpha/2)(\sigma)/(√(n))`

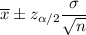
, where
`\overline{x}` = Sample mean

`\sigma` = Population standard deviation

`z_(\alpha/2)` = Critical z-value.

Substitute all the given values, then the required confidence interval will be :

`98\pm (1.96)(12)/(√(36))`

`=98\pm (1.96)(12)/(6)`

`=98\pm (1.96)(2)`

`=98\pm 3.92=(98-3.92,\ 98+3.92)\\\\=( 94.08,\ 101.92)`

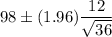
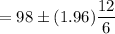
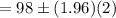
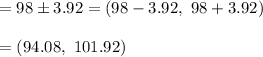
Therefore, the 95% confidence interval for the mean of x is (94.08, 101.92) .