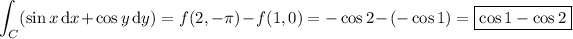Direct computation:
Parameterize the top part of the circle
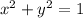 by
by

with
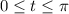 , and the line segment by
, and the line segment by
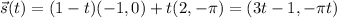
with
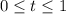 . Then
. Then
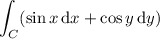
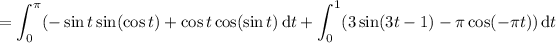
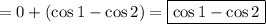
Using the fundamental theorem of calculus:
The integral can be written as
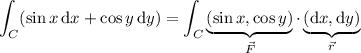
If there happens to be a scalar function
 such that
such that
 , then
, then
 is conservative and the integral is path-independent, so we only need to worry about the value of
is conservative and the integral is path-independent, so we only need to worry about the value of
 at the path's endpoints.
at the path's endpoints.
This requires

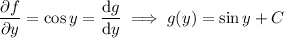
So we have
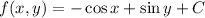
which means
 is indeed conservative. By the fundamental theorem, we have
is indeed conservative. By the fundamental theorem, we have