Answer:
Tension, T = 0.1429 N
Step-by-step explanation:
Given that,
Mass of the rock, m = 0.0450 kg
Radius of the circle, r = 0.580 m
Angular speed,
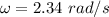
The tension in the string is balanced by the centripetal force acting on it. It is given by :
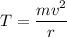
Since,
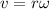
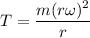
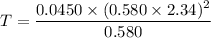
T = 0.1429 N
So, the tension in the string is 0.1429 N. Hence, this is the required solution.