Question

From an observation deck, Matt spots two deer to the right of the observation deck, standing 108 feet apart in a field below. The angles of depression to each of the deer are 15o20’ and 36o17’. How high is the observation deck he is standing on?

Answer 1

The height of the observation deck is approximately 47.266 feet.

Explanation:

We include a geometrical representation of the statement in the image attached below. Let be O the location of the observation deck, and A and B the locations of the two deers, which are 108 feet apart of each other. By knowing that sum of internal angles within triangle equals 180º. The angles O, B and A are now determined:

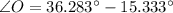
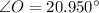
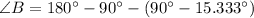
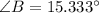
`\angle O = 36.283^(\circ)-15.333^(\circ)`

`\angle O = 20.950^(\circ)`

`\angle B = 180^(\circ)-90^(\circ)-(90^(\circ)-15.333^(\circ))`

`\angle B = 15.333^(\circ)`

`\angle A = 180^(\circ)-\angle O - \angle B` (1)

`\angle A = 180^(\circ)-20.950^(\circ)-15.333^(\circ)`

`\angle A = 143.717^(\circ)`

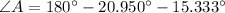
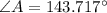
By the law of Sine we determine the length of the segment OB:

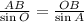`(AB)/(\sin O) = (OB)/(\sin A)` (2)

`OB = \left((\sin A)/(\sin O)\right)\cdot AB`

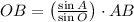
If we know that
`\angle A = 143.717^(\circ)`,
`\angle O = 20.950^(\circ)` and
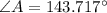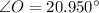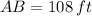`AB = 108\,ft`, then the length of the segment OB is:

`OB = \left((\sin 143.717^(\circ))/(\sin 20.950^(\circ)) \right)\cdot (108\,ft)`

`OB \approx 178.747\,ft`

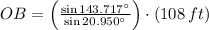
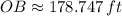
Lastly, we determine the height of the observation deck by the following trigonometric identity:

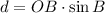`d = OB\cdot \sin B` (3)

If we know that
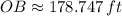`OB \approx 178.747\,ft` and
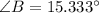`\angle B = 15.333^(\circ)`, then the height of the observation deck is:

`d = (178.747\,ft)\cdot \sin 15.333^(\circ)`

`d\approx 47.266\,ft`

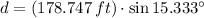
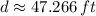
The height of the observation deck is approximately 47.266 feet.