Question

A certain radioactive nuclide decays with a disintegration constant of 0.0178 h-1.

(a) Calculate the half-life of this nuclide.

What fraction of a sample will remain at the end of (b) 4.44 half-lives and (c) 14.6 days?

Answer 1

Step-by-step explanation:

Given that,

The disintegration constant of the nuclide,
`\lambda=0.0178\ h^(-1)`

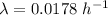
(a) The half life of this nuclide is given by :

`t_(1/2)=(ln(2))/(\lambda)`

`t_(1/2)=(ln(2))/(0.0178)`

`t_(1/2)=38.94\ h`

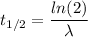
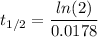
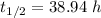
(b) The decay equation of any radioactive nuclide is given by :

`N=N_oe^(-\lambda t)`

`(N)/(N_o)=e^(-\lambda t)`

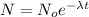
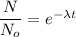
Number of remaining sample in 4.44 half lives is :

`t_(1/2)=4.44* 38.94`

`t_(1/2)=172.89\ h^(-1)`

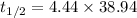
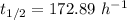
So,
`(N)/(N_o)=e^(-0.0178* 172.89)`

`(N)/(N_o)=0.046`

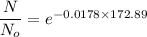
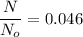
(c) Number of remaining sample in 14.6 days is :

`t_(1/2)=14.6* 24`

`t_(1/2)=350.4\ h^(-1)`

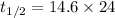
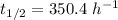
So,
`(N)/(N_o)=e^(-0.0178* 350.4)`

`(N)/(N_o)=0.0019`

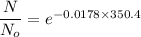
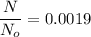
Hence, this is the required solution.