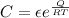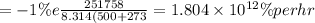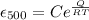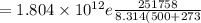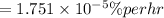Answer:
a) Q = 251.758 kJ/mol
b) creep rate is
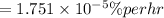
Step-by-step explanation:
we know Arrhenius expression is given as
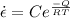
where
Q is activation energy
C is pre- exponential constant
At 700 degree C creep rate is
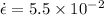 % per hr
% per hr
At 800 degree C creep rate is
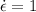 % per hr
% per hr
activation energy for creep is
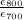 =
=
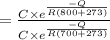
![(1\%)/(5.5 * 10^(-2)\%) = e^{[(-Q)/(R(800+273))] -[(-Q)/(R(800+273))]}](https://img.qammunity.org/2020/formulas/engineering/college/2jj050vy2ai60veboj3xlbhd0pa6p6z5io.png)
![(0.01)/(5.5* 10^(-4)) = ln [e^{(Q)/(8.314)[(1)/(1073) - (1)/(973)]}]](https://img.qammunity.org/2020/formulas/engineering/college/jbndgzwegnlr6d5kharvoj8984tkngguq2.png)
solving for Q we get
Q = 251.758 kJ/mol
b) creep rate at 500 degree C
we know