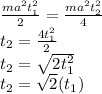Answer:
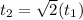
Step-by-step explanation:
The kinetic energy of a body is that energy it possesses due to its motion. In classical mechanics, this energy depends only on its mass and speed, as follows:
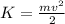
The speed in an uniformly accelerated motion is given by:
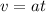
Replacing this expression in the formula for the kinetic energy, we have:
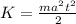
So, if we have
 :
:
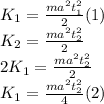
Equaling (1) and (2) and solving for
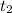 :
: