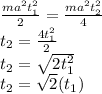Question

An object is acted upon by a constant force which gives it a constant acceleration a. At a certain time t1, having started from rest at t = 0, it has kinetic energy K1. At what time t2 has its kinetic energy doubled?

Answer 1

`t_2=√(2)(t_1)`

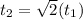
Step-by-step explanation:

The kinetic energy of a body is that energy it possesses due to its motion. In classical mechanics, this energy depends only on its mass and speed, as follows:

`K=(mv^2)/(2)`

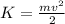
The speed in an uniformly accelerated motion is given by:

`v=at`

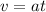
Replacing this expression in the formula for the kinetic energy, we have:

`K=(ma^2t^2)/(2)\\`

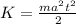
So, if we have
`K_2=2K_1`:

`K_1=(ma^2t_1^2)/(2)(1)\\K_2=(ma^2t_2^2)/(2)\\2K_1=(ma^2t_2^2)/(2)\\K_1=(ma^2t_2^2)/(4)(2)\\`

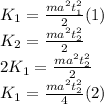
Equaling (1) and (2) and solving for
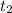`t_2`:

`(ma^2t_1^2)/(2)=(ma^2t_2^2)/(4)\\t_2=(4t_1^2)/(2)\\t_2=√(2t_1^2)\\t_2=√(2)(t_1)`