Question

Farmer Pickles wants Bob to paint the circular fence which encloses his sunflower field. If the parametric equations x = 18 cos(θ) and y = 18 sin(θ) describe the base of the fence (in yards) and the height of the fence is given by the equation h(x, y) = 12 + (2x − y)/6, then how many gallons of paint will Bob need to complete the project. Assume that one gallon of paint covers three hundred square feet of fence.

Answer 1

40.72 gallons

Explanation:

Since
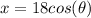`x = 18cos(\theta)` and
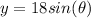`y = 18sin(\theta)`. We can say this base has a shape of a circle of radius r = 18.

We can also calculate h in term of angle θ:

`h(\theta) = 12 + (36cos(\theta) - 18sin(\theta))/(6)`

`h(\theta) = 12 + 6cos(\theta) - 3sin(\theta)`

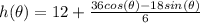
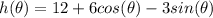
We can calculate the area of the fence if we integrate this h function over θr, which is the chord length. θ ranges from 0 to 2π

A = ∫h(θ)rdθ

A = ∫(12 + 6cos(θ) - 3sin(θ))18d

A = (12θ + 6sin(θ) + 3cos(θ))18

As θ ranges from 0 to 2π as a full circle

A = (12*0 + 6sin(0) + 3cos(0))18 - (12*2π + 6sin(2π) + 3cos(2π))18

A = 3*18 - 18(24π + 3) = 1357.17 square yard

As 1 yard = 3 feet then 1 square yard = 9 square feet

1 gallon of paint can cover 300 square feet or 300 / 9 = 33.33 square yard

So to cover square yard Bob would need

1357.17 / 33.33 = 40.72 gallons of paint.