Question

A rectangle has a length of 34 inches less than 5 times it’s width. If the area of the rectangle is 867 square inches, find the length of the rectangle.

Answer 1

Length of the rectangle is 51 inches

Solution:

Given that

Length of the rectangle in 34 miles less than 5 times its width

Area of rectangle = 867 square inches

Need to determine length of the rectangle.

Let assume width of the rectangle be represented by variable x.

So 5 times width of the rectangle =5x

34 inches less than 5 times width of the rectangle = 5x – 34

As Length of the rectangle in 34 miles less than 5 times its width

=> Length of the rectangle = 5x – 34

The formula for rectangle is given as:

`\text { area of rectangle }=length * width`

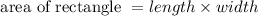
As given that Area of rectangle = 867 square inches

`\begin{array}{l}{=>867=(5 x-34) *(x)} \\\\ {=>5 x^(2)-34 x-867=0}\end{array}`

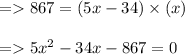
On solving quadratic equation by using quadratic formula

`x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

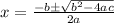
In our case a = 5, b = -34 and c = -867

On substituting value of a, b and c in quadratic formula we get

`\begin{array}{l}{x=\frac{-(-34) \pm \sqrt{(-34)^(2)-4 * 5 *(-867)}}{2 * 5}} \\\\ {=>x=(34 \pm √(18496))/(10)=(34+136)/(10)} \\\\ {=>x=(34+136)/(10)=17 \text { or } x=(34-136)/(10)=-10.2}\end{array}`

Since x represents width, it cannot be negative, so x = 17

Length of the rectangle = 5x – 34 = 5(17) – 34 = 51

Hence length of the rectangle is 51 inches