Answer:
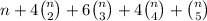
Explanation:
Lets divide it in cases, then sum everything
Case (1): All 5 numbers are different
In this case, the problem is reduced to count the number of subsets of cardinality 5 from a set of cardinality n. The order doesnt matter because once we have two different sets, we can order them descendently, and we obtain two different 5-tuples in decreasing order.
The total cardinality of this case therefore is the Combinatorial number of n with 5, in other words, the total amount of possibilities to pick 5 elements from a set of n.
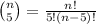
Case (2): 4 numbers are different
We start this case similarly to the previous one, we count how many subsets of 4 elements we can form from a set of n elements. The answer is the combinatorial number of n with 4
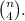
We still have to localize the other element, that forcibly, is one of the four chosen. Therefore, the total amount of possibilities for this case is multiplied by those 4 options.
The total cardinality of this case is
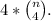
Case (3): 3 numbers are different
As we did before, we pick 3 elements from a set of n. The amount of possibilities is
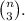
Then, we need to define the other 2 numbers. They can be the same number, in which case we have 3 possibilities, or they can be 2 different ones, in which case we have
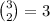 possibilities. Therefore, we have a total of 6 possibilities to define the other 2 numbers. That multiplies by 6 the total of cases for this part, giving a total of
possibilities. Therefore, we have a total of 6 possibilities to define the other 2 numbers. That multiplies by 6 the total of cases for this part, giving a total of
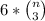
Case (4): 2 numbers are different
We pick 2 numbers from a set of n, with a total of
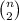 possibilities. We have 4 options to define the other 3 numbers, they can all three of them be equal to the biggest number, there can be 2 equal to the biggest number and 1 to the smallest one, there can be 1 equal to the biggest number and 2 to the smallest one, and they can all three of them be equal to the smallest number.
possibilities. We have 4 options to define the other 3 numbers, they can all three of them be equal to the biggest number, there can be 2 equal to the biggest number and 1 to the smallest one, there can be 1 equal to the biggest number and 2 to the smallest one, and they can all three of them be equal to the smallest number.
The total amount of possibilities for this case is
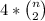
Case (5): All numbers are the same
This is easy, he have as many possibilities as numbers the set has. In other words, n
Conclussion
By summing over all 5 cases, the total amount of possibilities to form 5-tuples of integers from 1 through n is
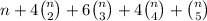
I hope that works for you!