Question

If n is a positive integer, how many 5-tuples of integers from 1 through n can be formed in which the elements of the 5-tuple are written in decreasing order but are not necessarily distinct? In other words, how many 5-tuples of integers (h, i, j, k, m) are there with n ≥ h ≥ i ≥ j ≥ k ≥ m ≥ 1?

Answer 1

`n + 4 {n \choose 2} + 6 {n \choose 3} + 4 {n \choose 4} + {n \choose 5}`

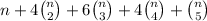
Explanation:

Lets divide it in cases, then sum everything

Case (1): All 5 numbers are different

In this case, the problem is reduced to count the number of subsets of cardinality 5 from a set of cardinality n. The order doesnt matter because once we have two different sets, we can order them descendently, and we obtain two different 5-tuples in decreasing order.

The total cardinality of this case therefore is the Combinatorial number of n with 5, in other words, the total amount of possibilities to pick 5 elements from a set of n.

`{n \choose 5 } = (n!)/(5!(n-5)!)`

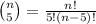
Case (2): 4 numbers are different

We start this case similarly to the previous one, we count how many subsets of 4 elements we can form from a set of n elements. The answer is the combinatorial number of n with 4
`{n \choose 4} .`

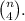
We still have to localize the other element, that forcibly, is one of the four chosen. Therefore, the total amount of possibilities for this case is multiplied by those 4 options.

The total cardinality of this case is
`4 * {n \choose 4} .`

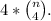
Case (3): 3 numbers are different

As we did before, we pick 3 elements from a set of n. The amount of possibilities is
`{n \choose 3} .`

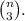
Then, we need to define the other 2 numbers. They can be the same number, in which case we have 3 possibilities, or they can be 2 different ones, in which case we have
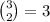`{3 \choose 2 } = 3` possibilities. Therefore, we have a total of 6 possibilities to define the other 2 numbers. That multiplies by 6 the total of cases for this part, giving a total of
`6 * {n \choose 3}`

Case (4): 2 numbers are different

We pick 2 numbers from a set of n, with a total of
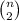`{n \choose 2}` possibilities. We have 4 options to define the other 3 numbers, they can all three of them be equal to the biggest number, there can be 2 equal to the biggest number and 1 to the smallest one, there can be 1 equal to the biggest number and 2 to the smallest one, and they can all three of them be equal to the smallest number.

The total amount of possibilities for this case is

`4 * {n \choose 2}`

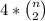
Case (5): All numbers are the same

This is easy, he have as many possibilities as numbers the set has. In other words, n

Conclussion

By summing over all 5 cases, the total amount of possibilities to form 5-tuples of integers from 1 through n is

`n + 4 {n \choose 2} + 6 {n \choose 3} + 4 {n \choose 4} + {n \choose 5}`

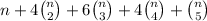
I hope that works for you!