Question

Water flows through a horizontal 60 mm diameter galvanized iron pipe at a rate of 0.02 m3/s. If the pressure drop is 135 kPa per 10 m of pipe, do you think this pipe is

a) a new pipe,
b) an old pipe with somewhat increased roughness due to aging or
c) a very old pipe that is partially clogged by deposits. Justify your answer.

Answer 1

pipe is old one with increased roughness

Step-by-step explanation:

discharge is given as

`V =(Q)/(A) = ( 0.02)/(\pi \4 * (60* 10^(-3))^2)`

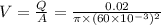
V = 7.07 m/s

from bernou;ii's theorem we have

`(p_1)/(\gamma)  +(V_1^2)/(2g) + z_1 = (p_2)/(\gamma)  +(V_2^2)/(2g) + z_2 + h_l`

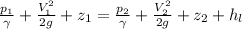
as we know pipe is horizontal and with constant velocity so we have

`P_1 -P_2 = (flv^2)/(2gD) * \gamma`

`135 * 10^3 = (f * 10* 7.07^2)/(2* 9.81 * 60 * 10^(-5)) * 1000 * 9.81`

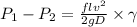
solving for friction factor f

f = 0.0324

fro galvanized iron pipe we have
`\epsilon  = 0.15 mm`

`(\epsilon)/(d) = (0.15)/(60) = 0.0025`

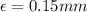
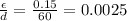
reynold number is

`Re =(Vd)/(\\u) = (7.07 * 60* 10^(-3))/(1.12* 10^(-6))`

Re = 378750

from moody chart

`For Re = 378750 and (\epsilon)/(d) = 0.0025`

`f_(new) = 0.025`

therefore new friction factor is less than old friction factoer hence pipe is not new one

now for Re = 378750 and f = 0.0324

from moody chart

we have
`(\epsilon)/(d) =0.006`

`\epsilon = 0.006 * 60`

`\epsilon = 0.36 mm`

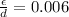
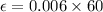
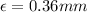
thus pipe is old one with increased roughness