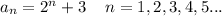Question

Consider the sequence:

5, 7, 11, 19, 35,....

Write an explicit definition that defines the sequence:



a_n = 2n + 3

a_n = 3n + 2

a_n = 3n^2

a_n = 2^n + 3

Answer 1

Answer:
`a_n = 2^n + 3\ \ \ \, n=1,2,3,4,5...`

Explanation:

The given sequence = 5, 7, 11, 19, 35,....

`7-5=2\\11-7=4=2^2\\19-11=8=2^3\\35-19=16=2^4`

Here , it cam be observe that the difference between the terms is not common but can be expressed as power of 2.

We can write the terms of the sequence as

`2^1+3=5\\2^2+3=4+3=7\\2^3+3=8+3=11\\2^4+3=16+3=19\\2^5+3=32+3=35`

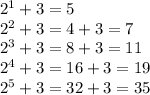
Then , the required explicit definition that defines the sequence will be

`a_n = 2^n + 3\ \ \ \, n=1,2,3,4,5...`

Answer 2

a_n = 2^n + 3

Explanation:

The first differences have a geometric progression, so the explicit definition will be an exponential function. (It cannot be modeled by a linear or quadratic function.) The above answer is the only choice that is an exponential function.

__

First differences are ...

(7-5=)2, 4, 8, 16