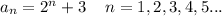Answer:
Explanation:
The given sequence = 5, 7, 11, 19, 35,....
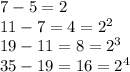
Here , it cam be observe that the difference between the terms is not common but can be expressed as power of 2.
We can write the terms of the sequence as
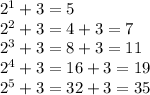
Then , the required explicit definition that defines the sequence will be