Question

An proton-antiproton pair is produced by a 2.20 × 10 3 2.20×103 MeV photon. What is the kinetic energy of the antiproton if the kinetic energy of the proton is 161.90 MeV? Use the following Joules-to-electron-Volts conversion 1eV = 1.602 × 10-19 J. The rest mass of a proton is 1.67 × 10 − 27 1.67×10−27 kg.

Answer 1

To solve this problem it is necessary to apply the concepts related to Kinetic Energy in Protons as well as mass-energy equivalence.

By definition the energy in a proton would be given by

The mass-energy equivalence is given as,

`E = mc^2`

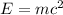
Here,

`m = mass(1.67*10^(-27) kg)`

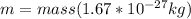
c = Speed of light
`(3*10^8m/s)`

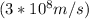
The energy of the photon is given by,

`E = 2*E_0 = 2*(m c^2)`

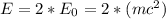
Replacing with our values,

`E = 2 (1.67*10^(-27)kg) (3*10^8m/s)^2`

`E = 3.006*10^(-10) J`

`E = 3.006*10^(-10) J((6.242*10^(12)MeV)/(1J))`

`E = 1876.34MeV`

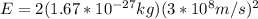
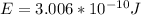
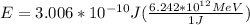
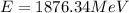
Therefore we can calculate the kinetic energy of an anti-proton through the energy total, that is,

`Etotal = E + KE_(proton) + KE_(antiproton)`

`(2200 MeV) = (1876.6 MeV) + (161.9 MeV) + KE_(antiproton)`

`(2200 MeV) = (2038.5 MeV) + KE_(antiproton)`

`KE_(antiproton) = (2200 MeV) - (2038.5 MeV)`

`KE_(antiproton) = 161.5 MeV`

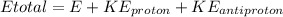
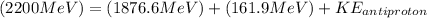
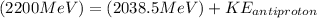
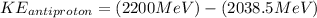
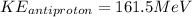
Therefore the kinetic energy of the antiproton if the kinetic energy of the proton is 161.90 MeV would be 161.5MeV