To solve this problem it is necessary to apply the concepts related to Kinetic Energy in Protons as well as mass-energy equivalence.
By definition the energy in a proton would be given by
The mass-energy equivalence is given as,
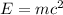
Here,
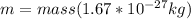
c = Speed of light

The energy of the photon is given by,
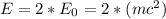
Replacing with our values,
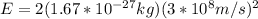
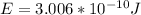
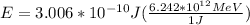
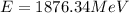
Therefore we can calculate the kinetic energy of an anti-proton through the energy total, that is,
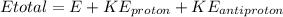
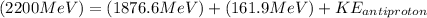
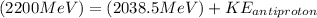
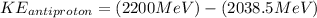
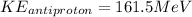
Therefore the kinetic energy of the antiproton if the kinetic energy of the proton is 161.90 MeV would be 161.5MeV