Question

The area of a square is decreasing at a rate of 43 square inches per second. At the time when the side length of the square is 7, what is the rate of change of the perimeter of the square? Round your answer to three decimal places (if necessary).

Answer 1

Answer: -12.286 in/sec

Explanation:

Differentiate A=s^2 to get d(A)/d(t) = 2s * d(s)/d(t).

Plug in -43 for d(A)/d(t) since it is the rate of change for area. Plug in 7 for s since it is the value of the side length. -43 = 2(7) * d(s)/d(T).

d(s)/d(T) equals -3.0714286

Differentiate P=4s to get d(P)/d(t) = 4 * d(s)/d(t)

Plug in -3.0714286 to d(P)/d(t) = 4 * d(s)/d(t).

d(P)/d(s)= -12.286 in/sec

Answer 2

26.230 Inches per second.

Explanation:

Since, Area of square is decreasing at the rate of 43 square inches per second And area is directly proportional to square of the side , So

Its side will be decreasing at the rate of
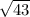`√(43)` inches per second .

Now,

Perimeter of square is directly proportional to 4 times of the side of the square.

so Perimeter of square will be decreasing at the rate of 4×
`√(43)`

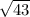
After rounding off to three decimal places we will get 26.230 Inches per second.