8 solid iron sphere with radius 'a cm' each are melted to form a sphere with radius 'b cm' then the ratio of a:b is 1 : 2
Solution:
Given that 8 solid iron sphere with radius 'a cm' each are melted to form a sphere with radius 'b cm'
Need to find the ratio of a:b
As 8 solid iron sphere with radius 'a cm' each are melted to form a sphere with radius 'b cm'.
For sake of simplicity, let volume of 1 sphere of radius a cm is represented by
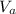 and volume of 1 sphere of radius b cm is represented by
and volume of 1 sphere of radius b cm is represented by
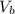
So volume of 8 solid iron sphere with radius 'a cm' = volume of 1 solid iron sphere with radius 'b cm'
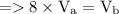
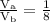 ---- eqn 1
---- eqn 1
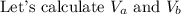
Formula for volume of sphere is as follows:

Where r is radius of the sphere
Substituting r = a cm in the formula of volume of sphere we get
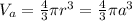
Substituting r = b cm in the formula of volume of sphere we get
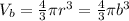
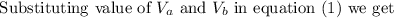


a : b = 1 : 2
Hence the ratio of a:b is 1 : 2