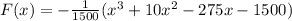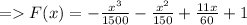Answer:
A

B
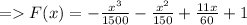
Explanation:
Function and its graphs
Part A
The graph shown in the image corresponds to a cubic function because of its classical infinite branches, three real roots and two extrema values
Part B
Knowing the value of the three roots x=-20, x=-5, and x=15 we can express the cubic function in factored form:
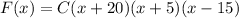
The value of C will be determined by using any particular point from the graph. Let's use (0,1)
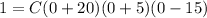
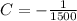
Replacing, we find the factored form of the function

The standard form demands to expand all the products and simplify