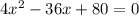Question

Write the quadratic equation whose roots are 4 and 5, and whose leading coefficient is 4.

Answer 1

The quadratic equation with the given roots of 4 and 5, and leading coefficient of 4, is 4(x - 4)(x - 5) = 0.

Step-by-step explanation:

Quadratic equations are of the form
`ax^2 + bx + c = 0.`

To find the equation with given roots, we can use the factoring method.

Since the roots are 4 and 5, the factors will be (x - 4) and (x - 5) respectively.

Multiplying these factors, we get the quadratic equation (x - 4)(x - 5) = 0.

To match the leading coefficient of 4, we can multiply both sides of the equation by 4, resulting in the quadratic equation 4(x - 4)(x - 5) = 0.

Answer 2

The quadratic equation whose roots are 4 and 5, and whose leading coefficient is 4 is
`4 x^(2)-36 x+80=0`

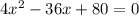
Solution:

Given that, roots of an quadratic equation are 4 and 5.

We have to find the equation of the quadratic equation.

Now, as 4 and 5 are roots, x = 4 and x = 5

Which means x – 4 and x – 5 are factors of the quadratic equation.

Then, equation will be the products of the factors

So, equation is (x - 4)(x - 5) = 0

Upon multiplication we get,

`\begin{array}{l}{x(x-5)-4(x-5)=0} \\\\ {x^(2)-5 x-4 x+20=0} \\\\ {x^(2)-9 x+20=0}\end{array}`

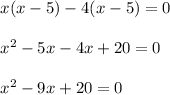
As we are given that, leading coefficient of the equation is 4. So multiply equation with 4

`\begin{array}{l}{\rightarrow 4\left(x^(2)-9 x+20=0\right)} \\\\ {\rightarrow 4 x^(2)-36 x+80=0}\end{array}`

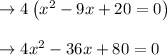
Hence, the quadratic equation is
`4 x^(2)-36 x+80=0`