Question

X=16.2 cos(4.68t+0.420). What is the velocity of the oscillator at t=7.97 s?

Answer 1

If using radians: 16.2

If using degrees: 12.8

Don't forget your units

Step-by-step explanation:

I assume that x represents the velocity?

If so, then just substitute the value t and solve

Answer 2

Assuming that the angle is in radians, the velocity of the oscillator at
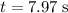`t = \rm 7.97 \; s` would be equal to approximately
`\rm -1.55`.

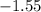Step-by-step explanation:

Assume that the
`x` here stands for the displacement of the oscillator from its equilibrium position at time
`t`.

Velocity is the first derivative of displacement with respect to time. So is the case in this question. Differentiate the expression for
`x` with respect to
`t` to find the velocity at time
`t`:

`v(t) = (d)/(dt) [x(t)] = (d)/(dt) [16.2\,  \cos(4.68 \, t + 0.420)]= 16.2 \, (d)/(dt) [16.2\,  \cos(4.68 \, t + 0.420)]`.

In calculus,
`(d)/(dt) \,[\cos(f(t))] = - \sin(t) \cdot (d)/(dt)[f(t)]` by the chain rule. In this case the inner function is
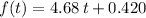`f(t) = 4.68 \, t + 0.420`. Its first derivative is equal to
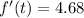`f^(\prime)(t) = 4.68`. Hence

`(d)/(dt) [\cos(4.68 \, t + 0.420)] = - \sin(4.68\, t + 0.420) \cdot 4.68 = -4.68\, \sin(4.68\, t + 0.420)`.

Therefore

`v(t) = -(4.68 * 16.2) \, \sin(4.68 \, t + 0.420)`.

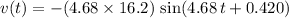At time
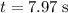`t = \rm 7.97\; s`, that would be equal to

`-16.2 * 4.68 \cdot \sin(4.68 * 7.97 + 0.420) \approx \rm 1.55`.

Hence the (linear) velocity of the oscillator at
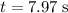`t = \rm 7.97 \; s` would be equal to
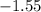`\rm -1.55`.