Question

Write the equation of each line using the given information.

a. The points (-4,1) and (2,4) both lie on the line
b. m= -1 and the point (2,-1) lies on the line
c. It has the same slope as y = 5 and passes through (1,1)
d. m= -3 and it has a y-intercept of (0,8)

Answer 1

a) x – 2y + 6 = 0 b) x + y = 1 c) y = 1 d) y = -3x + 8

Solution:

a. The points (-4,1) and (2,4) both lie on the line

The general line equation on which (a, b) and (c, d) lies is:

`y-\mathrm{b}=(d-b)/(c-a)(x - a)`

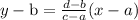
Here the given points are (a, b) = (-4, 1) and (c, d) = (2, 4)

Thus the required equation is:

`y-1=(4-1)/(2-(-4))(x-(-4))`

On solving we get,

`\begin{array}{l}{\rightarrow y-1=(3)/(2+4)(x+4)} \\\\ {\rightarrow y-1=(3)/(6)(x+4)} \\\\ {\rightarrow 2(y-1)=1(x+4)} \\\\ {\rightarrow 2 y-2=x+4} \\\\ {\rightarrow x-2 y+6=0}\end{array}`

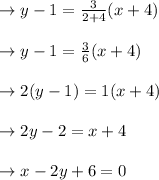
b.) m= -1 and the point (2, -1) lies on the line

The equation of line in point slope form is y – b = m(x – a)

where m is slope and (a, b) is a point on it

Here m = -1 and (a, b) = (2, -1)

Thus the required equation is:

y – (-1) = -1(x - 2)

y + 1 = -x + 2

y = -x + 2 -1

y = -x + 1

c. )It has the same slope as y = 5 and passes through (1, 1)

our line has same slope with y = 5, then our equation would be y = k and it passes through (x, y) = (1, 1) so, then by substitution

1 = k

k =1

Then our equation will be y = k

y = 1

d. ) m= -3 and it has a y-intercept of (0, 8)

line equation in slope intercept form is y = mx + b where m is slope and b is y – intercept.

Then, our equation will be y = -3x + 8

We took y- intercept = 8 as it is the value of y when x = 0