11 pounds of apples for $40.59 Equation: t = $3.69n. 12 gallons of gasoline for $44.16 Equation: t = $3.68n. 15 magazines for $54.75 Equation: t = $3.65n. 14 sandwiches for $50.68 Equation: t = $3.62n with arrowBoth.
To match the proportional relationships to their corresponding equations:
1. 11 pounds of apples for $40.59
- The cost per pound is
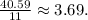
- Equation: t = $3.69n
2. 12 gallons of gasoline for $44.16
- The cost per gallon is

- Equation: t = $3.68n
3. 15 magazines for $54.75
- The cost per magazine is

- Equation: t = $3.65n
4. 14 sandwiches for $50.68
- The cost per sandwich is
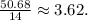
- Equation: t = $3.62n
In each case, the equation t = kn represents the proportional relationship, where k is the constant unit rate of cost per item. The arrowBoth indicates the direction of the proportional relationship.