Question

20 points for this question:

Find the domain.

Answer 1

The Domain D = {y ∈ R / y ≠
`(b)/(2)` y ≠ 0}

Explanation:

Let ,

f(y) =
`(b^(2) - 4by )/(2y^(2) - by )` -
`(4y)/(b-2y)`

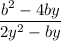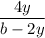
The above function would be defined only when the denominator of anyone or both the terms of the function do not become 0 -

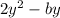`2y^(2) - by` ≠ 0 and b - 2y ≠ 0

∴ y(2y - b) ≠ 0 and y ≠
`(b)/(2)`

Either y ≠ 0 or y ≠
`(b)/(2)`

∵ The domain of a function consists of only those points where the function is defined -

The Domain D consists of all y ∈ Real numbers such that y ≠ 0 and y ≠
`(b)/(2)`